[জিওগ্রাফিক ইনফরমেশন সিস্টেম (GIS) – লেকচার ৩]
[জিওগ্রাফিক ইনফরমেশন সিস্টেম (GIS) – লেকচার ৫]
স্থানাঙ্ক ব্যবস্থা (পর্ব-২)
গত লেকচারে (লেকচার – ৩) আমরা ‘স্থানাঙ্ক ব্যবস্থা’ নিয়ে আলোচনা শুরু করেছি। এই লেকচারে আমরা আরও নতুন কিছু জানতে চেষ্টা করব।
পূর্ব কথাঃ
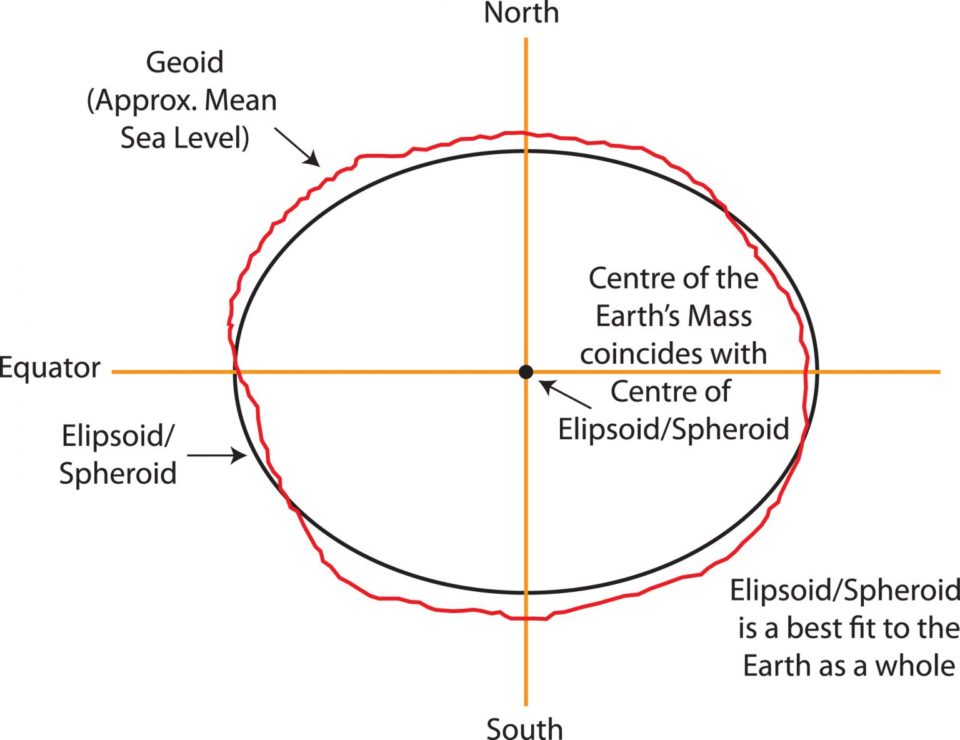
যেহেতু পৃথিবীর বিভিন্ন স্থানের ভর (Mass) ভিন্ন এবং মাধ্যাকর্ষণ (Gravity) এর অভিমুখ (Direction) পরিবর্তনশীল তাই ‘ভূগোলক (Geoid)’- এর আকার অনিয়মিত।
তাই গাণিতিক হিসাব সহজে করার জন্য, একটি ভৌগলিক স্থানাঙ্ক ব্যবস্থায় পৃথিবী পৃষ্ঠের (Surface) আকার ও আকৃতি, একটি ‘গোলক’ (Sphere) বা ‘উপগোলক’ (Ellipsoid/Spheroid) দ্বারা সংজ্ঞায়িত করা হয়।
এখন প্রশ্ন হল, কখন আমরা পৃথিবীকে ‘গোলক’ এবং কখন ‘উপগোলক’ হিসাবে বিবেচনা করব? এটি নির্ভর করে, মানচিত্র তৈরির উদ্দেশ্য এবং নির্ভুল তথ্যের (Data Accuracy) উপর।
উদাহরণস্বরূপ বলা যায়, যদি আমরা অনেক বড় বা বিশাল এলাকা (Area) একটি ছোট স্থানে উপস্থাপন করতে চায় তাহলে পৃথিবীকে ‘গোলক’ হিসাবে বিবেচনা করা হয়। যেমনঃ ‘বিশ্বের মানচিত্র’ (World Map) বা ‘আঞ্চলিক মানচিত্র’ (Regional Map)।
আবার যদি আমরা একটি ছোট এলাকাকে বিস্তারিতভাবে (more detail) দেখতে চায়, তাহলে পৃথিবীকে ‘উপগোলক’ হিসাবে বিবেচনা করা হয়। যেমনঃ একটি দেশের বা শহরের মানচিত্র (Country/City Map)।
যেহেতু সচরাচর আমরা একটি ছোট এলাকা নিয়ে কাজ করে থাকি এবং মানচিত্রের সঠিকতা/ যথাযথতা (Precision/Accuracy) নিয়ে বেশি উদ্বিগ্ন থাকি; সেহেতু ‘জিআইএস’-এ সাধারণত পৃথিবীকে একটি ‘উপগোলক’ (Ellipsoid/Spheroid) হিসাবেই সংজ্ঞায়িত করা হয়।
এইবার গোলক এবং উপগোলকের গঠনতন্ত্র নিয়ে কিছুটা আলোচনা করা যাক।
পৃথিবী যখন উপবৃত্তাকার (Ellipsoid) বা উপগোলক (Spheroid)
নিচের ছবিতে আমরা একটি ডিম্বাকৃতি ‘উপবৃত্ত’ (Ellipse) দেখতে পারছি। এই উপবৃত্তের আকৃতি দুইটি অক্ষ দ্বারা নির্ধারিত হয়। এর প্রধান/বড় অক্ষকে বলা হয় ‘Major Axis’ এবং অপেক্ষাকৃত ছোট/খাটো অক্ষকে বলা হয় ‘Minor Axis’। ‘Semi-Major Axis’ দৈর্ঘ্যে ‘Major Axis’-এর অর্ধেক এবং ‘Semi-Minor Axis’ দৈর্ঘ্যে ‘Minor Axis’-এর অর্ধেক।
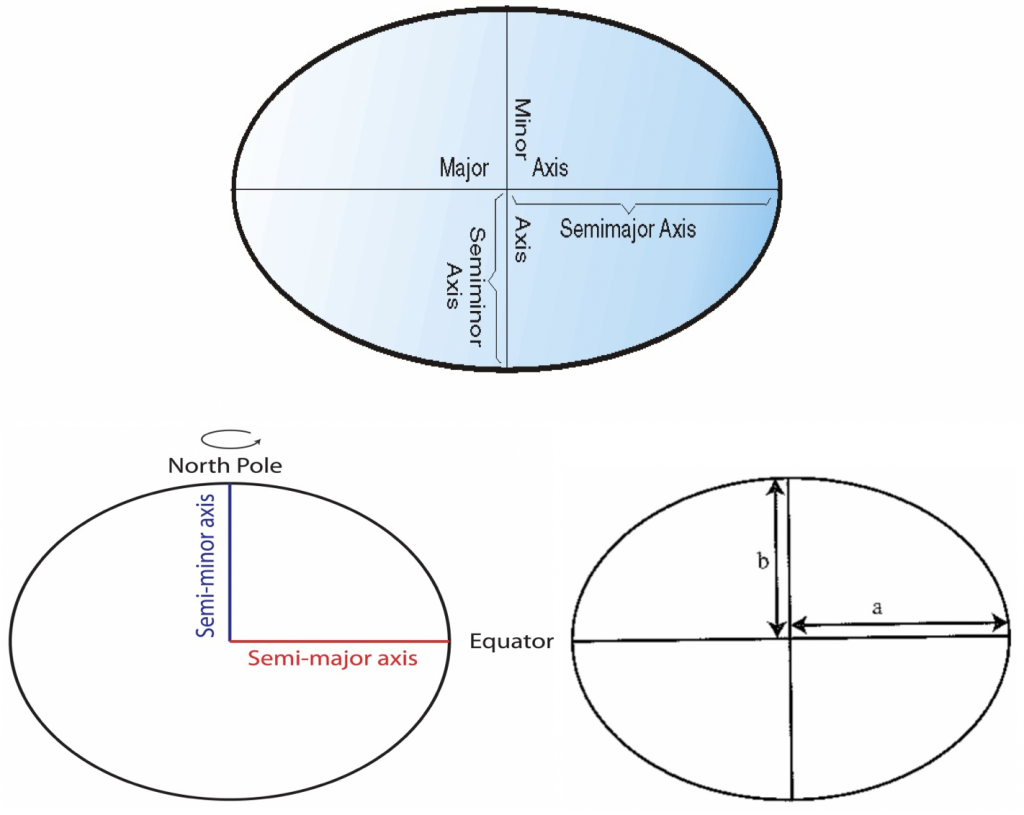
একটি ‘Ellipsoid’ এর নিম্নলিখিত পরামিতি (Parameters) আছেঃ
Semi-Major অক্ষ = a
Semi-Minor অক্ষ = b; যেখানে a > b
সমরূপতা (Flattening), f = [‘Flattening’ এর পরিসর ‘0’ থেকে ‘১’ এর মধ্যে হয়]
বিপরীত সমরূপতা (Inverse Flattening) = 1 / f
উত্কেন্দ্রতা (Eccentricity), e2 = (a2-b2) / a2; e2 = 2f – f2
এই উপবৃত্তকে তার যে কোন একটি অক্ষ (Axis) বরাবর আবর্তিত (Rotate) করালে যে ত্রিমাত্রিক আকৃতি গঠিত হয় তাকেই ‘Ellipsoid’ বা ‘Spheroid’ বলে। সহজ কথায়, একটি ‘উপগোলক’ হল একটি ত্রিমাত্রিক আকৃতি যা একটি দ্বি-ত্রিমাত্রিক ‘উপবৃত্ত’ থেকে তৈরি। নিচের ছবিটি দেখুন।
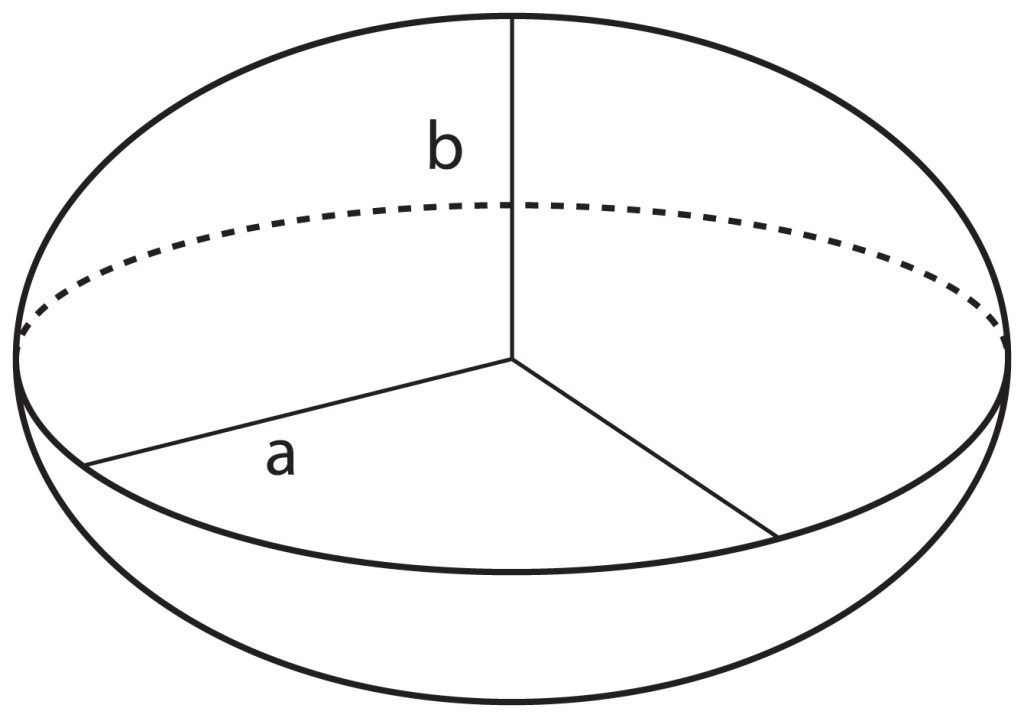
পৃথিবী যখন গোলক (Sphere)
যখন ‘a = b’, বা ২ টি অক্ষ সমান অর্থাৎ ‘Flattening’ শূন্য হয় তখন ফলাফল হবে একটি ‘গোলক’। নিচের ছবিটি দেখুন।
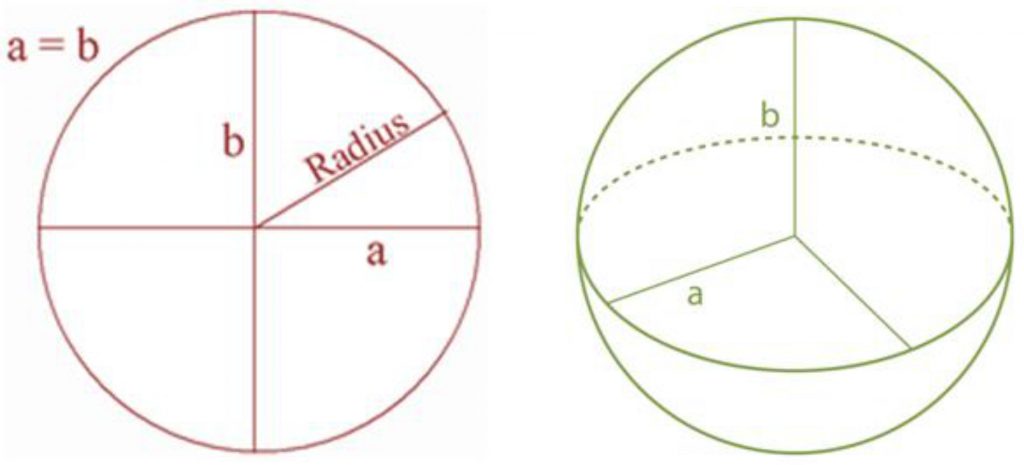
এর মানে হল, ‘Flattening’ যত শূন্যের (০) কাছাকাছি হবে আকৃতি ততই গোলাকার হবে। আর ‘Flattening’ এর মান যতই ‘১’-এর কাছাকাছি হবে আকৃতি হবে ততই উপবৃত্তাকার।
জেনে রাখা ভাল যে পৃথিবীর ‘Flattening’ হল আনুমানিক ০.০০৩৩৫৩। এর মানে হল পৃথিবীর আকৃতি গোলকের খুব কাছাকাছি হলেও কিছুটা উপবৃত্তাকার।
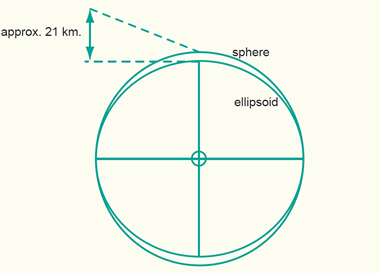
উপরের এই ছবিটি পৃথিবীর ‘Ellipsoid’ এবং ‘Sphere’-এর মধ্যকার পার্থক্য বুঝতে সাহায্য করবে।
একটাই পৃথিবী, কিন্তু ‘Ellipsoid’ অনেক
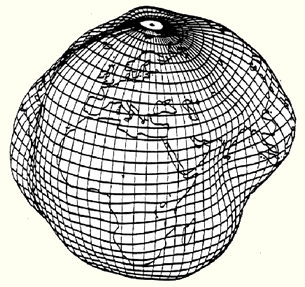
এইবার কাহিনী আছে, আসলে এককভাবে কোন ‘Ellipsoid’-ই পৃথিবীর আকৃতির (Geoid) সাথে পুরোপুরি মিলে যায় না। কোথাও মিলে যায়, আবার কোথাও আংশিকভাবে মিলে। উদাহরণস্বরূপ নিচের ছবিটি দেখুন।
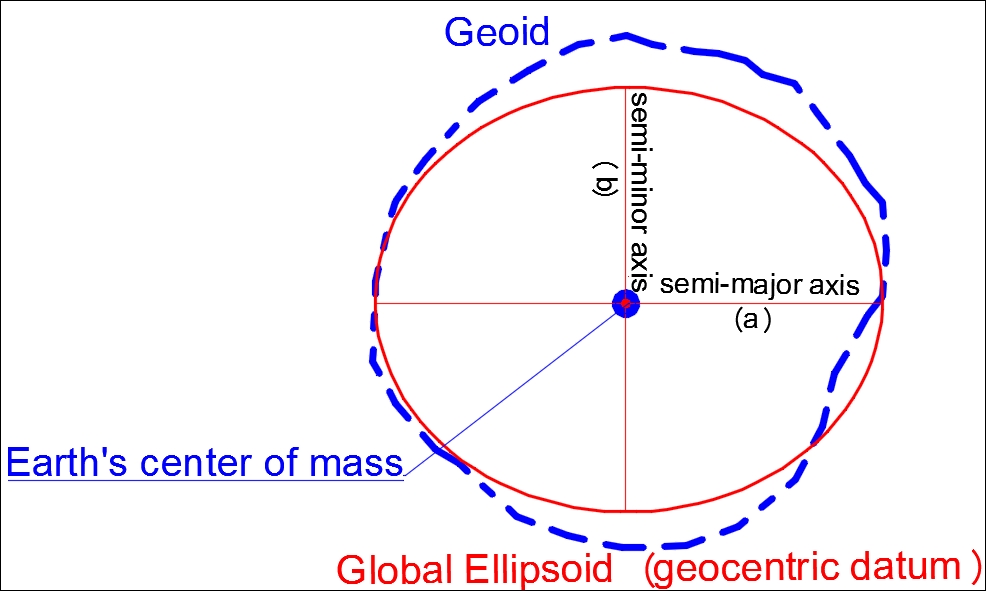
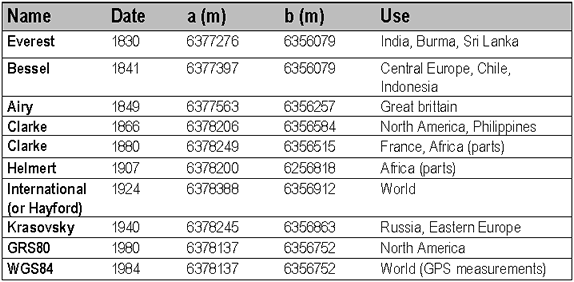
বিগত দুই শতাব্দী ধরে, পৃথিবীর সাথে খাপ খায় (Best-Fitting) এইরকম প্রায় কয়েকশত ‘Ellipsoid’ হিসাব করে বের করা হয়েছে। কিন্তু এর মধ্যে মাত্র কয়েকটি বর্তমানে মানচিত্রের কাজে ব্যবহৃত হচ্ছে। নিম্নে এইরকম বহুল ব্যবহৃত কয়েকটি ‘Ellipsoid’-এর পরামিতিসমূহ উল্লেখ করা হলঃ
সহজ কথায়, একটি নির্দিষ্ট ভৌগলিক এলাকার জন্য একটি নির্দিষ্ট ‘উপগোলক’ (Ellipsoid) ব্যবহার করা যেতে পারে। কিন্তু ঐ উপগোলক সমগ্র পৃথিবী বা অন্যান্য এলাকার জন্য উপযুক্ত নাও হতে পারে।
Datum
এইবার আমরা ‘Datum’ বা ‘Geodetic Datum’ বা ‘Reference Datum’ কি তা জানতে চেষ্টা করব। ‘Datum’ হল এমন এক ধরণের পদ্ধতি (Mechanism) যার মাধ্যমে ‘Ellipsoid’ এবং ‘Geoid’-এর মধ্যকার সম্পর্ক নিরূপণ করা হয়। ‘Datum’-
১. পৃথিবীর কেন্দ্রে উপগোলকের (Ellipsoid) আপেক্ষিক অবস্থান নির্ধারণ করে।
২. অক্ষাংশ ও দ্রাঘিমাংশ রেখাসমূহের উৎপত্তি (Origin) এবং অভিযোজন (Orientation) নির্দেশ করে।
৩. একটি ত্রিমাত্রিক তল (Three Dimensional Surface) যার মাধ্যমে অক্ষাংশ, দ্রাঘিমাংশ এবং উচ্চতা (Elevation/Height) গাণিতিকভাবে হিসাব/ নির্ণয় করা যায়।
ভূপৃষ্ঠের সাথে খাপ খাওয়ানোর জন্য যেমন বিভিন্ন ধরণের গাণিতিক মডেল আছে, তেমনি বিভিন্ন ধরণের ‘Datum’-ও আছে। ‘Datum’ এবং ‘Ellipsoid’ এক নয়। ‘Datum’-এর জ্যামিতিক কাঠামোই হল ‘Ellipsoid’। অর্থাৎ ‘Ellipsoid’ হল একটি জ্যামিতিক আকৃতি এবং ‘Datum’ হল ঐ নির্দিষ্ট আকৃতির উপাত্ত।
কোন একটি স্থানের স্থানাঙ্ক, ‘Ellipsoid’ এবং ‘Datum’-এর উপর নির্ভরশীল। ‘Datum’-এর অবস্থান পরিবর্তন করা হলে ‘X’, ‘Y’ ও ‘Z’-ও পরিবর্তিত হবে। সহজ কথায়, ‘Datum’ পরিবর্তন করা মানেই হল ‘ভৌগোলিক স্থানাঙ্ক ব্যবস্থা’র (Geographic Coordinate System) পরিবর্তন করা।
তিনটি ভিন্ন ভিন্ন ‘Datum’-এর জন্য একটি শহরের ‘ভৌগোলিক স্থানাঙ্ক’ ভিন্ন ভিন্ন হতে পারে। উদাহরণস্বরূপ, নিচের টেবিলটি দেখুনঃ
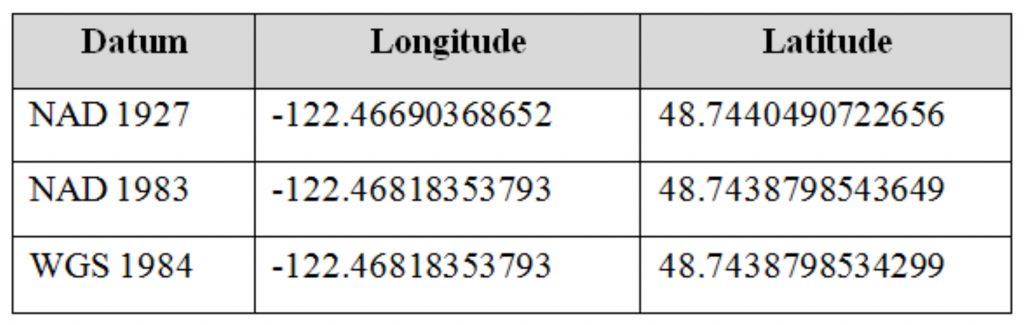
আবার একই ‘Ellipsoid’ বিশিষ্ট ভিন্ন ভিন্ন ‘Datum’-এর জন্য একটি নির্দিষ্ট স্থানের ভৌগোলিক স্থানাঙ্ক বিভিন্ন হতে পারে (Datum Shift)। নিচের ছবিটি দেখুনঃ
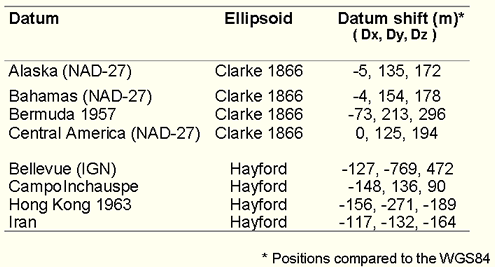
তাই এইটা বলা যায় যে শুধুমাত্র ‘Ellipsoid’ এর উপর ভিত্তি করে সঠিক ‘Datum’ বের করা সম্ভব না। অন্যভাবে বলা যায়, ‘Datum’ সম্পর্কে জানা থাকলে ‘Ellipsoid’ সহজেই নির্ধারণ করা সম্ভব।
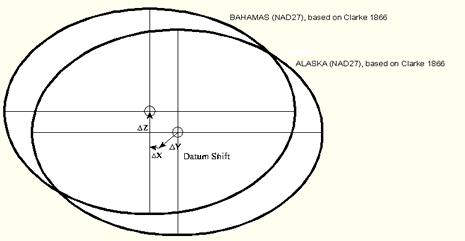
একইভাবে নিচের ছবিটি দেখে আমরা বুঝতে পারছি যে একই ‘Ellipsoid’ থাকা সত্ত্বেও (Clarke 1866), ‘Datum’ (= ‘X’, ‘Y’ ও ‘Z’) ভিন্ন হওয়ার কারণে (Bahamas NAD-27 এবং Alaska NAD-27)একটি নির্দিষ্ট স্থানের ভৌগোলিক অবস্থান পরিবর্তিত হয়েছে (Datum Shift)।
স্থানীয়/ আঞ্চলিক Datum
ভূপৃষ্ঠের কোন নির্দিষ্ট এলাকা বা অঞ্চলের সাথে উপগোলককে খুব কাছাকাছি মিলানোর জন্য “স্থানীয়/ আঞ্চলিক Datum” ব্যবহৃত হয়। এক্ষেত্রে উপগোলকের তলের কমপক্ষে একটি নির্দিষ্ট বিন্দুর সাথে ভূপৃষ্ঠের কোন নির্দিষ্ট অংশ মিলে যায়। যেই বিন্দুতে ভূপৃষ্ঠ এবং উপগোলক মিলিত হয় তাকে ঐ ‘Datum’-এর ‘Origin Point’/ ‘উৎস বিন্দু’ বলে। ‘Origin Point’-এর স্থানাঙ্ক অনড় (Fixed)। এই ‘Origin Point’-এর উপর ভিত্তি করেই গাণিতিকভাবে অন্যান্য সকল বিন্দুর স্থানাঙ্ক নির্ণয় করা হয়।
নিচের ছবিটি “স্থানীয়/আঞ্চলিক Datum” এর একটি উদাহরণ। ছবিটিতে দেখা যাচ্ছে যে পৃথিবীর প্রকৃত ভরকেন্দ্র (Centre of the Earth’s Mass) এবং ‘Ellipsoid’-এর কেন্দ্র ভিন্ন। এছাড়াও ‘Ellipsoid’টি ভূপৃষ্ঠের একটি নির্দিষ্ট অংশের সাথে ভালভাবে মিশে গিয়েছে, কিন্তু অন্যান্য অংশের সাথে যথেষ্ট অসামঞ্জস্যপূর্ণ।
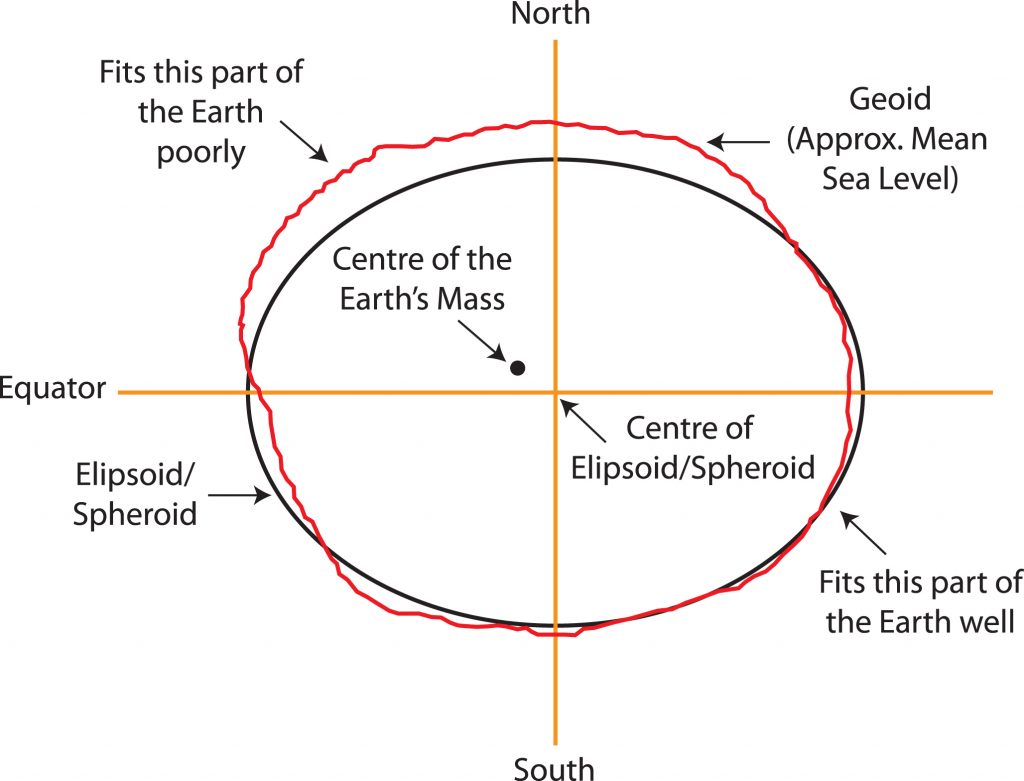
একটি নির্দিষ্ট স্থানের জন্য নির্ধারিত “স্থানীয়/আঞ্চলিক Datum” অন্য স্থানের জন্য ব্যবহার করলে তা ভুল স্থানাঙ্ক প্রদর্শন করবে।
ভূকেন্দ্রিক Datum
‘ভূকেন্দ্রিক/Geocentric Datum’-এর ক্ষেত্রে পৃথিবীর প্রকৃত ভরকেন্দ্র এবং ‘Ellipsoid’-এর কেন্দ্র একই অবস্থানে থাকে। এক্ষেত্রে এমন একটি ‘Ellipsoid’ বেছে নেয়া হয়, যেটা সমগ্র পৃথিবীর আকৃতির সাথে যথাসম্ভব নিখুঁতভাবে মিশে যায়। নিচের ছবিটি ‘Geocentric Datum’-এর একটি সুন্দর উদাহরণ।
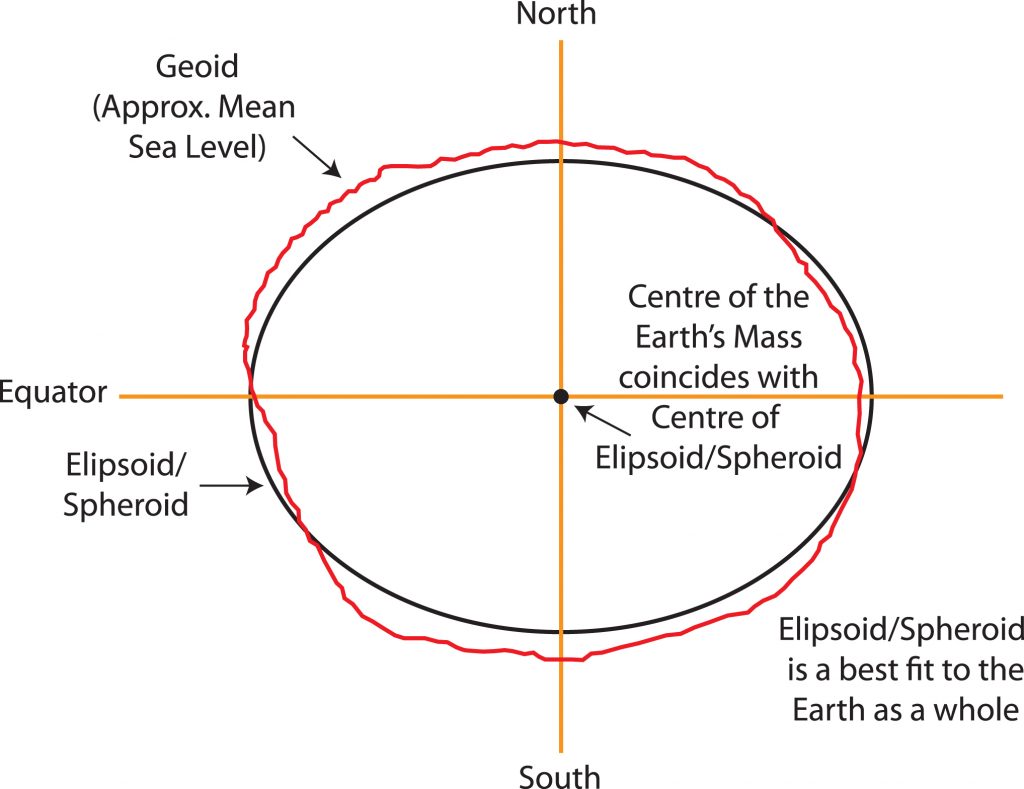
বর্তমান সময়ে বহুলভাবে ব্যবহৃত ‘Geocentric Datum’ হল- ‘World Geodetic System 1984’ বা ‘WGS84’। ‘Geocentric Datum’ পৃথিবীর যে কোন স্থানের ভৌগোলিক অবস্থান নির্ণয়ে ব্যবহৃত হতে পারে।
নিচের চিত্রে আরও কিছু সংখ্যক ‘Datum’ এবং সংশ্লিষ্ট ‘Ellipsoid/Spheroid’-এর বর্ণনা তুলে ধরা হলঃ
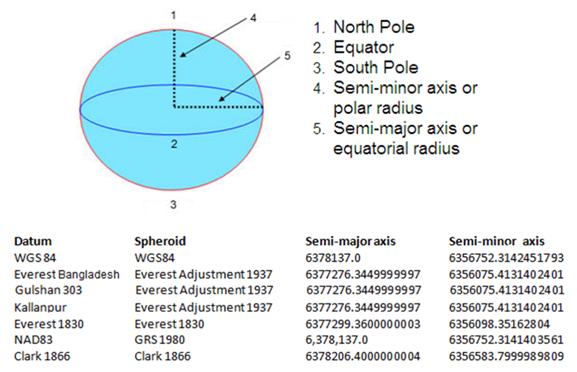
বর্তমান সময়ে জ্ঞান-বিজ্ঞানের প্রভূত উন্নয়ন এবং মানুষের মাঝে সচেতনতা বৃদ্ধির কারণে, সবাই ভূপৃষ্ঠে কোন কিছুর অবস্থার খুবই নির্ভুলভাবে বের করতে সচেষ্ট। ভৌগোলিক অবস্থান নির্ণয়ে সামান্য হের-ফের (Small Difference) বড় ধরণের সমস্যা সৃষ্টি করতে পারে।
এইসব কারণে, খুবই নিখুঁতভাবে কোন কিছুর ভৌগোলিক অবস্থান নির্ণয়ের জন্য ভূ-বিজ্ঞানীরা বিভিন্ন ধরণের ‘Ellipsoid/Spheroid’ এবং ‘Datum’ ব্যবহার করেন।
‘ভৌগোলিক স্থানাঙ্ক ব্যবস্থা’ (Geographic Coordinate System) নিয়ে কথা-বার্তা এখানেই শেষ করছি। আগামী লেকচারে ‘অভিক্ষিপ্ত স্থানাঙ্ক ব্যবস্থা’ (Projected Coordinate System) নিয়ে বিস্তারিত আলোচনা করার ইচ্ছা আছে।
ধন্যবাদ, সবাই ভাল থাকবেন।