[জিওগ্রাফিক ইনফরমেশন সিস্টেম (GIS) – লেকচার ৬]
[জিওগ্রাফিক ইনফরমেশন সিস্টেম (GIS) – লেকচার ৮]
মানচিত্র অভিক্ষেপের প্রকারভেদ (পর্ব- ১)
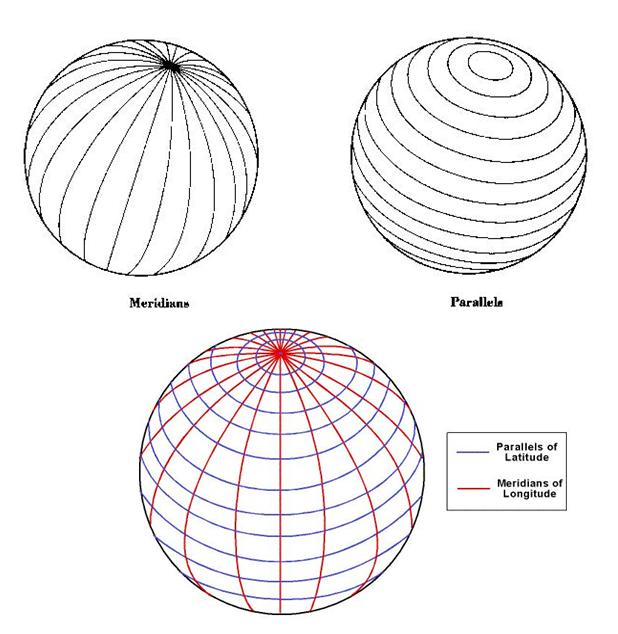
আজকের লেকচারের প্রথমেই ‘মধ্য-রেখা’ (Meridian) এবং ‘সমান্তরাল’ (Parallel) কি, তা আবার স্মরণ করার চেষ্টা করি নিম্নের ছবিটি দেখেঃ
আমাদেরকে প্রথমেই জানতে হবে, কেন ‘GIS’-এ বিভিন্ন ধরণের মানচিত্র অভিক্ষেপ ব্যবহার করা হয়? সহজ উত্তর হল- পৃথিবীর অসম আকৃতির (বৃত্তাকার/ গোলাকার) কারণে, বিভিন্ন এলাকার সঠিক ও নির্ভুল মানচিত্র-অঙ্কনের জন্যই এসব বিভিন্ন অভিক্ষেপ ব্যবহৃত হয়। প্রতিটি অভিক্ষেপেরই নিজস্ব সুবিধা এবং অসুবিধাসমূহ আছে। কোন অভিক্ষেপই পৃথিবীর সকল এলাকার জন্য প্রযোজ্য নয়। তাই নানাবিধ অভিক্ষেপ বিদ্যমান আছে।
মানচিত্র অভিক্ষেপ প্রধানত তিন প্রকারঃ-
- Conical [মোচাকৃতি]
- Cylindrical [বেলনাকার]
- Planar [সমতল]
নিম্নে এদের বিস্তারিত বর্ণনা দেয়া হলঃ
১) মোচাকৃতি অভিক্ষেপ (Conical Projections):
এই অভিক্ষেপের ধারণাটি হল- একটি কাগজের টুকরাকে আবর্তিত করে ‘Cone’ আকৃতি দেয়া। এর ফলে মোচাটি পৃথিবীকে বৃত্তাকারভাবে স্পর্শ করে।
যে অক্ষাংশ রেখায় ‘Cone’ এবং পৃথিবী পরস্পরকে স্পর্শ করে তাকে ‘Standard Parallel’ বলে। এরপর চূড়ান্ত অভিক্ষেপের জন্য মোচাটিকে যে কোন মধ্য-রেখা (Meridian) বরাবর কর্তন করা হয়।
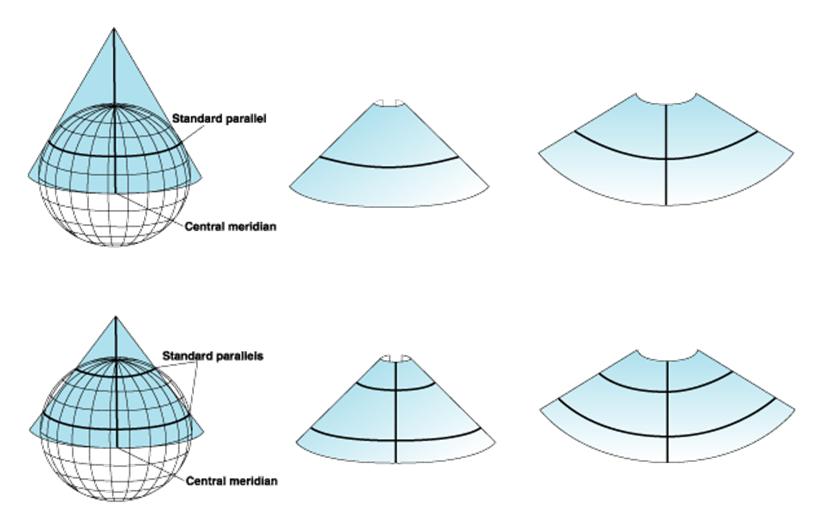
একটি ‘Standard Parallel’ থাকলে তা হল, ‘Tangent Conic Projection’ এবং দুইটি ‘Standard Parallel’ থাকলে তা হল ‘Secant Conic Projection’। নিচের ছবি দুইটি দেখুনঃ
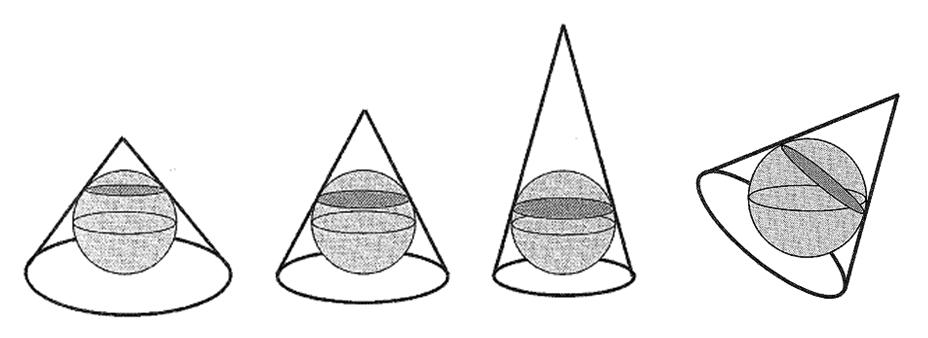
আবার মোচার (Cone) আকৃতি বিভিন্ন ধরণের হতে পারে। এর ফলে বিভিন্ন ধরণের ‘Standard Parallel’ সৃষ্টি হয়। এই ‘Cone’-এর আকৃতি নির্ধারণ করা হয় এমনভাবে যেন ‘Standard Parallel’ যেই এলাকার মানচিত্র অভিক্ষেপ/অঙ্কন করা হবে, তার মধ্য দিয়ে অতিক্রম করে। নিচের ছবিটি দেখুনঃ
মোচাকৃতি অভিক্ষেপের (Conical Projections) আবার প্রকারভেদ আছে। যেমনঃ
১.১) Equidistant Conic:
এই ক্ষেত্রে ‘Standard Parallel’ থেকে যতই দূরে যাওয়া যায়- অভিমুখ (Direction), ক্ষেত্র/ এলাকা (Area) এবং আকৃতি (Shape) ততই বিকৃত (Distort) হয়।
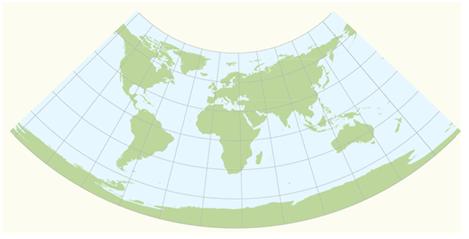
১.২) Albers Equal-Area Projection:
এই অভিক্ষেপে ক্ষেত্র/ এলাকার পরিমাপ ঠিক থাকে।
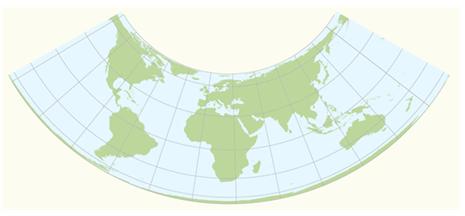
১.৩) Lambert Conformal Conic Projection:
এই ক্ষেত্রে ‘Standard Parallel’ থেকে যতই দূরে যাওয়া যায়- ক্ষেত্র/ এলাকা (Area) এবং আকৃতি (Shape) ততই বিকৃত (Distort) হয়।আর ক্ষেত্র বিশেষে অভিমুখ (Direction) ঠিক থাকে।
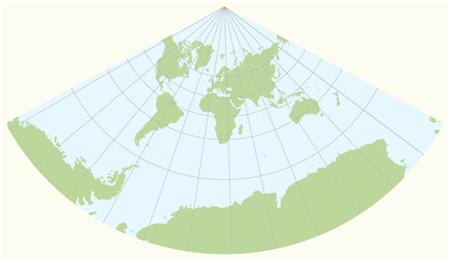
১.৪) Polyconic Projection:
এই ক্ষেত্রে মূল মধ্য-রেখা (Central Meridian) সোজা (Straight) এবং অন্যান্য মধ্য রেখাগুলো (Meridians) জটিল বক্র-রেখারূপে (Complex Curve) থাকে। এছাড়াও প্রতিটি সমান্তরাল (Parallel) এবং মূল মধ্য-রেখা বরাবর মানচিত্রের ‘Scale’ ঠিক থাকে।
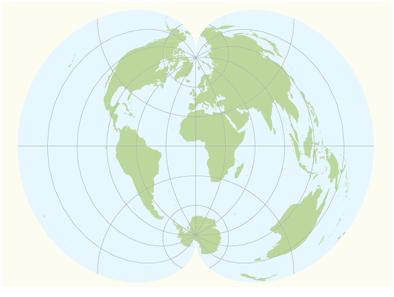
১.৫) Pseudo-Conical Projections:
এক্ষেত্রে মধ্য রেখাসমূহ বক্রাকার এবং শুধুমাত্র মূল মধ্য-রেখা (Central Meridian) সোজা থাকে। তবে সমান্তরালগুলো সমানভাবে ব্যবধানযুক্ত এককেন্দ্রিক (Equally Spaced Concentric) বৃত্তাকার চাপ (Circular Arcs) হিসাবে থাকে।
মোচাকৃতি অভিক্ষেপ (Conical Projections) সম্পর্কে আমরা এটুকুই জানব। আজকের মতো ‘লেকচার-৭’ এইখানেই শেষ করছি। পরবর্তী লেকচারে বেলনাকার (Cylindrical) এবং সমতল (Planar) অভিক্ষেপ নিয়ে আলোচনা করার চেষ্টা করব। ভাল থাকবেন, ধন্যবাদ!